若关于x的方程x2-4=x+m没有
若一元二次不等式2kx2+kx-38<0对
若一元二次不等式2kx2+kx- |
已知函数f(x)=12x2-mlnx+(
已知函数f(x)= |
(1)当m=2时,求函数f(x)的最小值; (2)当m≤0时,讨论函数f(x)的单调性; (3)求证:当m=-2时,对任意的x1,x2∈(0,+∞),且x1≠x2,有
若关于x的不等式x2-4x-2-a>0在区间(1
若关于x的不等式x2-4x-2-a>0在区间(1,4)内有解,则实数a的取值范围是( ) |
要使不等式kx2-kx+1>0对于x的任意值都成
要使不等式kx2-kx+1>0对于x的任意值都成立,则k的取值范围是______. | 函数f(x)=2x-x2,(0
函数f(x)= |
|

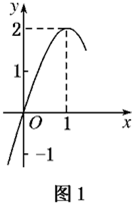 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.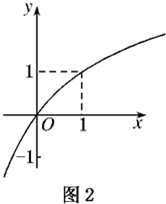
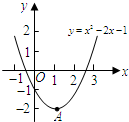
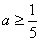
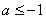
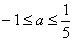
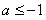 或
或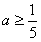
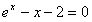 的一个根所在的区间为( )。
的一个根所在的区间为( )。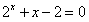 的解所在的区间是
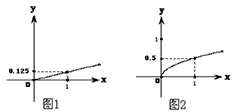
的解所在的区间是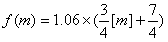 给出,其中m>0,[m]表示不大于m的最大整数(如[3]=3,[3.9]=3,[3.1]=3),则从甲城市到乙城市5.8分钟的电话费为( )。
给出,其中m>0,[m]表示不大于m的最大整数(如[3]=3,[3.9]=3,[3.1]=3),则从甲城市到乙城市5.8分钟的电话费为( )。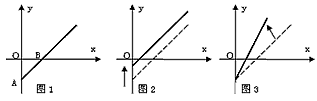
 ax-1为从集合A到B的映射,若f(2)=3,则f(3)=( )。
ax-1为从集合A到B的映射,若f(2)=3,则f(3)=( )。