题目
答案 |
| 当0≤x≤3,f(x)=2x-x2=-(x-1)2+1,对称轴为x=1,抛物线开口向下, ∵0≤x≤3, ∴当x=1时,函数f(x)最大为1,当x=3时,函数取得最小值-1, ∴-1≤f(x)≤1. 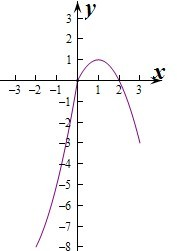 当-2≤x<0,f(x)=x2+6x=(x+3)2-9,对称轴为x=-3,抛物线开口向上, 且函数在[-2,0]上单调递增, ∴-8≤f(x)<0. 综上,-8≤f(x)≤1. 即函数的值域为[-8,1]. 故选:C. |
答案 |
| 当0≤x≤3,f(x)=2x-x2=-(x-1)2+1,对称轴为x=1,抛物线开口向下, ∵0≤x≤3, ∴当x=1时,函数f(x)最大为1,当x=3时,函数取得最小值-1, ∴-1≤f(x)≤1. 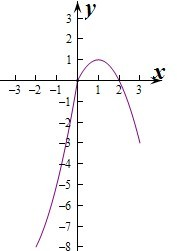 当-2≤x<0,f(x)=x2+6x=(x+3)2-9,对称轴为x=-3,抛物线开口向上, 且函数在[-2,0]上单调递增, ∴-8≤f(x)<0. 综上,-8≤f(x)≤1. 即函数的值域为[-8,1]. 故选:C. |