题目

已知函数f（x）=ln（e^x+a）（e是自然对数的底数，a为常数）是实数集R上的奇函数，若函数g（x）=lnx-f（x）（x²-2ex+m）在（0，+∞）上有两个零点，则实数m的取值范围是（　　）

A．（ 1 e ，e2+ 1 e ）

B．（0，e2+ 1 e ）

C．（e2+ 1 e ，+∞）

D．（-∞，e2+ 1 e ）

答案

∵函数f（x）=ln（e^x+a）是实数集R上的奇函数，
∴f（0）=0，即f（0）=ln（1+a）=0，解得a=0，即f（x）=lne^x=x．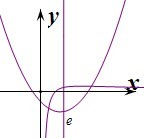
∴g（x）=lnx-f（x）（x²-2ex+m）=lnx-x（x²-2ex+m），
由g（x）=lnx-x（x²-2ex+m）=0，得

lnx

x

=x²-2ex+m，
设h（x）=

lnx

x

，m（x）=x²-2ex+m，
则m（x）=（x-e）²+m-e²≥m-e²，
h"（x）=

1-lnx

x2

，由h"（x）＞0，得0＜x＜e，此时函数单调递增，
由h"（x）＜0，得x＞e，此时函数单调递减，
∴当x=e时，函数h（x）取得最大值h（e）=

lne

e

=

1

e

，
要使g（x）=lnx-f（x）（x²-2ex+m）在（0，+∞）上有两个零点，
则

1

e

＞m-e2，即m＜

1

e

+e2．
故选D．

解析