定义域为R的偶函数f(x)满足对∀x∈R,有f(
难度:简单
题型:单选题
来源:不详
题目
定义域为R的偶函数f(x)满足对∀x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时f(x)=-2(x-3)2,若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则a的取值范围为( )
A.(0,
答案
| 由f(x+2)=f(x)-f(1)得f(x+2)+f(1)=f(x),以-x代x,得f(-x+2)+f(1)=f(-x),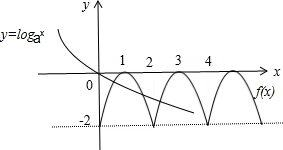
由于f(x)为偶函数,所以f(x)=f(-x),得出f(x+2)=f(-x+2)①,可知f(x)图象以x=2为对称轴.
在f(x+2)=f(x)-f(1),令x=-1,得出f(1)=f(-1)-f(1)=0,所以f(x+2)=f(x)周期T=2,
作出f(x)的图象,
∵y=loga(x+1)的图象与f(x)的图象至少有三个交点,即有loga(2+1)>f(2)=-2且0<a<1,解得a∈(0, |
| |
|