题目
答案 |
| 解:因为f(x-2)=f(x),所以函数y=f(x)(x∈R)是周期为2函数. 因为x∈[-1,1]时,f(x)=1-x2,所以作出它的图象, 利用函数y=f(x)(x∈R)是周期为2函数, 可作出y=f(x)在区间[-5,6]上的图象,如图所示: 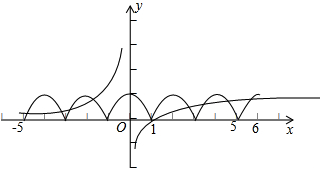 故函数h (x )=f (x )-g (x )在区间[-5 ,6] 内的零点的个数为9 , 故选C . |
答案 |
| 解:因为f(x-2)=f(x),所以函数y=f(x)(x∈R)是周期为2函数. 因为x∈[-1,1]时,f(x)=1-x2,所以作出它的图象, 利用函数y=f(x)(x∈R)是周期为2函数, 可作出y=f(x)在区间[-5,6]上的图象,如图所示:  故函数h (x )=f (x )-g (x )在区间[-5 ,6] 内的零点的个数为9 , 故选C . |