题目
(1)求数列{an}的通项公式;
(2)数列{bn}的前n项和为Tn,且bn=
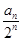 ,求Tn.
,求Tn.
答案
(2)Tn=-7-
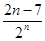
解析
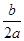 =5,当n≥2时,an=Sn-Sn-1=an2+bn-a(n-1)2-b(n-1)=2an+b-a=2an-11a.
=5,当n≥2时,an=Sn-Sn-1=an2+bn-a(n-1)2-b(n-1)=2an+b-a=2an-11a.∵a2=-7,得a=1.∴a1=S1=-9,∴an=2n-11.
(2)∵bn=
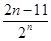 ,
,∴Tn=
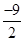 +
+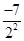 +…+
+…+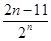 ,①
,①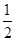 Tn=
Tn=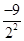 +…+
+…+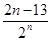 +
+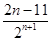 ,②
,②①-②得
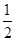 Tn=-
Tn=-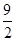 +
+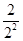 +…+
+…+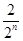 -
-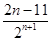
=-
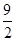 +
+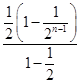 -
-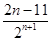
=-
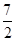 -
-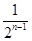 -
-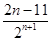 .
.∴Tn=-7-
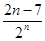 .
.
