题目
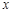 轴上的椭圆
轴上的椭圆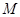 的离心率为
的离心率为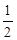 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点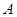 与左右两焦点
与左右两焦点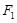 、
、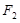 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为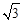 .
.(1)求椭圆
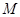 的标准方程;
的标准方程;(2)已知点
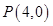 ,连接
,连接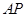 与椭圆的另一交点记为
与椭圆的另一交点记为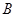 ,若
,若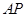 与椭圆相切时
与椭圆相切时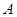 、
、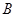 不重合,连接
不重合,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求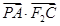 的取值范围.
的取值范围.
答案
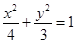 ;(2)
;(2)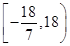 .
.
解析
试题分析:(1)先利用已知条件列举出有关
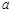 、
、 、
、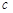 的方程组,结合三者之间满足的勾股关系求出
的方程组,结合三者之间满足的勾股关系求出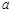 、
、 、
、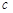 的值,从而确定椭圆的方程;(2)设直线
的值,从而确定椭圆的方程;(2)设直线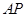 与
与 的方程分别为
的方程分别为 以及
以及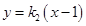 ,将两条直线方程与椭圆方程联立,结合韦达定理得到点
,将两条直线方程与椭圆方程联立,结合韦达定理得到点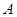 与点
与点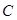 之间的关系(关于
之间的关系(关于 轴对称),从而得到两点坐标之间的关系,最后将
轴对称),从而得到两点坐标之间的关系,最后将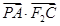 利用点
利用点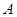 的坐标进行表示,注意到坐标的取值范围,然后利用二次函数求出
的坐标进行表示,注意到坐标的取值范围,然后利用二次函数求出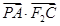 的取值范围.
的取值范围.(1)由题可知:
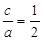 ,
,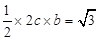 ,
,解得:
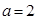 ,
,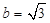 ,
,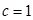 ,
,故椭圆
 的方程为:
的方程为: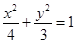 ;
;(2)不妨设
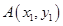 、
、 、
、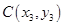 ,
,由题意可知直线
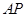 的斜率是存在的,故设直线
的斜率是存在的,故设直线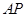 的斜率为
的斜率为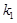 ,直线
,直线 的斜率为
的斜率为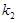
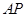 的方程为: 代入椭圆方程
的方程为: 代入椭圆方程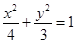 ,得
,得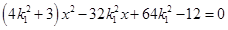 ,
,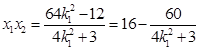 ,
,将
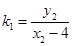 ,
,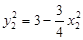 代入解得:
代入解得: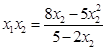 ,
, 的方程为:
的方程为: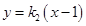 代入椭圆方程
代入椭圆方程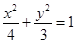 ,得
,得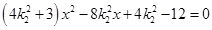 ,
,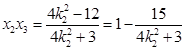 ,
,将
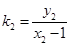 ,
,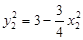 ,代入解得:
,代入解得: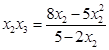 ,
,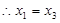 ,又
,又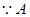 、
、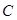 不重合,
不重合,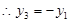 ,
,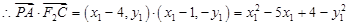
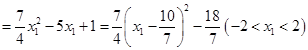 ,
,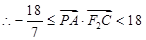 .
.
