题目

已知二次函数f(x)＝ax²＋bx＋c (a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，f(x)≤.
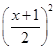(1)求f(1)的值；
(2)证明：a>0，c>0；
(3)当x∈[－1,1]时，函数g(x)＝f(x)－mx (x∈R)是单调函数，求证：m≤0或m≥1.

答案

（1）f(1)＝1. （2）见解析 （3）见解析

解析

(1)解　∵对x∈R，f(x)－x≥0恒成立，
当x＝1时，f(1)≥1，
又∵1∈(0,2)，由已知得f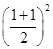(1)≤＝1，
∴1≤f(1)≤1.∴f(1)＝1.
(2)证明　∵f(1)＝1，∴a＋b＋c＝1.
又∵a－b＋c＝0，∴b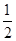＝.∴a＋c＝.
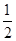∵f(x)－x≥0对x∈R恒成立，
∴ax²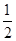－x＋c≥0对x∈R恒成立．
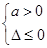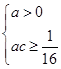∴，　∴∴c>0，故a>0，c>0.
(3)证明　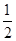∵a＋c＝，ac≥，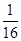
由a>0，c>0及a＋c≥2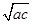，得ac≤，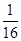
∴ac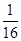＝，当且仅当a＝c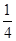＝时，取“＝”．
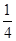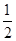∴f(x)＝x²＋x＋.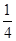
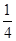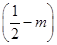∴g(x)＝f(x)－mx＝x²＋x＋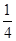
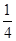＝[x²＋(2－4m)x＋1]．
∵g(x)在[－1,1]上是单调函数，
∴2m－1≤－1或2m－1≥1.∴m≤0或m≥1.