题目

(2014·孝感模拟)已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x²+2ax+1+a²,g(x)=x-+.
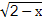(1)求函数f(x)的最小值.
(2)对于∀x₁,x₂∈[0,2],f(x₁)>g(x₂)恒成立,求实数a的取值范围.

答案

（1）f(x)_min=
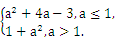
（2）a∈(-∞,-5)∪(1,+∞)

解析

(1)函数f(x)的对称轴是x=a,
当a≤1时,f(x)_min=f(2)=a²+4a-3,
当a>1时,f(x)_min=f(0)=1+a²,
所以f(x)_min=
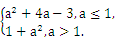
(2)令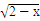=t(t∈[0,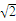]),则x=2-t²,
所以g(x)=h(t)=-t²+t+,
因为对称轴t=∈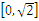,所以g(x)_max=h(t)_max=2,
由题意,要使对于∀x₁,x₂∈[0,2],f(x₁)>g(x₂)恒成立,只要f(x)_min>g(x)_max即可,
所以当a≤1时,f(x)_min=a²+4a-3>2,
解得：a<-5,
当a>1时,f(x)_min=1+a²>2,解得：a>1,
综上所述,a∈(-∞,-5)∪(1,+∞).