题目
(1)求a,b的值;
(2)若函数f(x)在x∈[m,1]上的最小值为1,求实数m的值.
答案
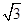
解析
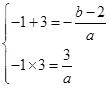 ,解得:a=-1,b=4.
,解得:a=-1,b=4.(2)f(x)=-x2+2x+3,对称轴方程为x=1,
∴f(x)在x∈[m,1]上单调递增.
∴x=m时,f(x)min=-m2+2m+3=1,
解得m=1±
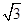 .∵m<1,∴m=1-
.∵m<1,∴m=1-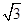 .
.
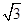
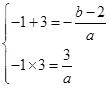 ,解得:a=-1,b=4.
,解得:a=-1,b=4.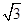 .∵m<1,∴m=1-
.∵m<1,∴m=1-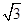 .
.