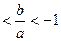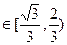题目
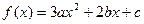 ,若a+b+c=0,f(0)f(1)>0,
,若a+b+c=0,f(0)f(1)>0,(1)求证:方程f(x)=0有实根;
(2)求证:-2
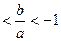 ;
;(3)设
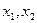 是方程f(x)=0的两个根,求
是方程f(x)=0的两个根,求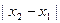 的取值范围
的取值范围
答案
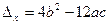 >0,所以所给方程有实根;(2)解此不等式得:-2
>0,所以所给方程有实根;(2)解此不等式得:-2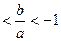 ;(3)
;(3) 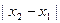
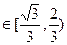
解析
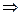 c(3a+2b+c)>0, 又a+b+c="0" 即c=-a-b
c(3a+2b+c)>0, 又a+b+c="0" 即c=-a-b所以(-a-b)(2a+b)>0即 2a
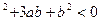
(1)
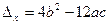 =4
=4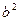 +12a(a+b)=12a
+12a(a+b)=12a +12ab+4b
+12ab+4b
=12[(a
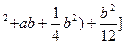 >0
>0
所以所给方程有实根。;
(2)由2a
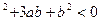 知
知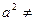 0,
0,且

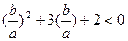 解此不等式得:-2
解此不等式得:-2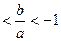
(3)|
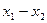 |=
|=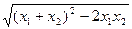 =
==
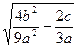
=
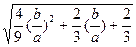 -2
-2