题目
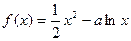
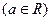
(1)若函数
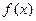 在
在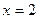 处的切线方程为
处的切线方程为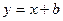 ,求
,求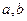 的值;
的值;(2)若函数
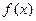 在
在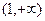 为增函数,求
为增函数,求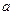 的取值范围;
的取值范围;(3)讨论方程
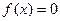 解的个数,并说明理由。
解的个数,并说明理由。
答案
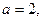
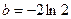 ;(2)
;(2)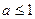 ;(3)当
;(3)当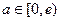 时,方程无解;当
时,方程无解;当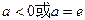 时,方程有惟一解; 当
时,方程有惟一解; 当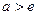 时方程有两解。
时方程有两解。
解析
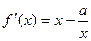
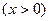 ,又
,又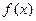 在
在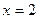 处的切线方程为
处的切线方程为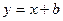
所以
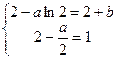 解得:
解得: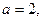
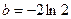
(2)若函数
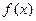 在
在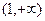 上恒成立。则
上恒成立。则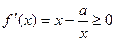 在
在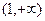 上恒成立,
上恒成立,即:
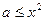 在
在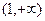 上恒成立。所以有
上恒成立。所以有 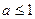
(3)当
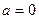 时,
时,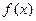 在定义域
在定义域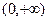 上恒大于
上恒大于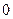 ,此时方程无解;
,此时方程无解;当
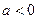 时,
时,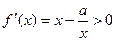 在
在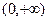 上恒成立,所以
上恒成立,所以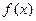 在定义域
在定义域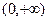 上为增函数。
上为增函数。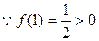 ,
,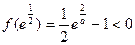 ,所以方程有惟一解。
,所以方程有惟一解。当
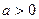 时,
时,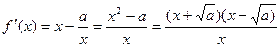
因为当
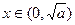 时,
时,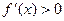 ,
,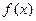 在
在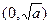 内为减函数;
内为减函数;当
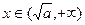 时,
时,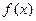 在
在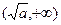 内为增函数。
内为增函数。所以当
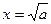 时,有极小值即为最小值
时,有极小值即为最小值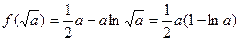 。
。当
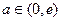 时,
时,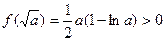 ,此方程无解;
,此方程无解;当
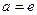 时,
时,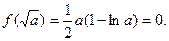 此方程有惟一解
此方程有惟一解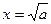 。
。当
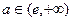 时,
时,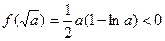
因为
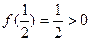 且
且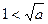 ,所以方程
,所以方程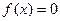 在区间
在区间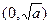 上有惟一解,
上有惟一解,因为当
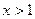 时,
时,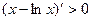 ,所以
,所以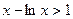
所以
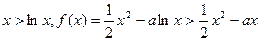
因为
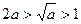 ,所以
,所以 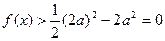
所以 方程
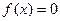 在区间
在区间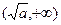 上有惟一解。
上有惟一解。所以方程
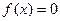 在区间
在区间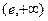 上有惟两解。
上有惟两解。综上所述:当
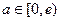 时,方程无解;当
时,方程无解;当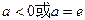 时,方程有惟一解;
时,方程有惟一解;当
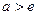 时方程有两解。
时方程有两解。
