题目
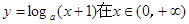 内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
答案
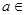
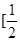 ,1
,1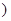
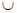 (
(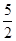 ,+
,+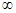 )
)
解析
试题分析:当0<a<1时,函数
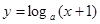 在(0,+
在(0,+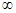 )内单调递减.
)内单调递减.当a>1时,
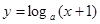 在(0,+
在(0,+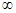 )内不是单调递减函数.
)内不是单调递减函数. ∴0<a<1
曲线y=x2+(2a-3)x+1与x轴交于不同的两点等价于(2a-3)2-4>0,即
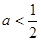 或
或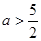 .
. 若p真q假,则
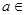 (0,1)
(0,1)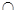 {
{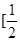 ,1
,1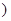
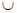
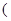 1,
1,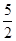 ]}=
]}=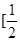 ,1
,1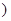 .
.若p假q真,注意到已知a>0,a≠1,所以有
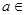 (1,+
(1,+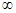 )
)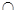 {(0,
{(0,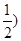
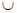 (
(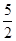 ,+
,+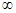 )
)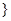 =(
=(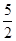 ,+
,+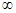 )
)综上可知,
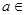
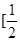 ,1
,1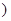
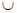 (
(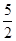 ,+
,+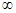 ).
).点评:本题考查了对数函数的单调性、二次函数根的判定及否命题的知识.
