题目
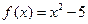 的一个正零点(误差不超过
的一个正零点(误差不超过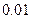 ).
).
答案
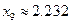 可作为所求函数的一个正零点的近似值
可作为所求函数的一个正零点的近似值
解析
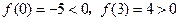 ,可取区间
,可取区间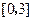 作为计算的初始区间.
作为计算的初始区间.用二分法逐次计算,列表如下:
| 端点(中点)坐标 |
计算中点的函数值 |
取区间 |
| |
|
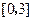 |
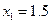 |
 |
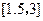 |
 |
 |
 |
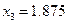 |
 |
 |
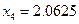 |
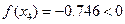 |
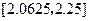 |
 |
 |
 |
 |
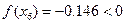 |
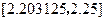 |
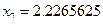 |
 |
 |
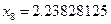 |
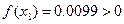 |
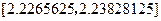 |
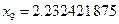 |
|
|
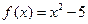 的一个正零点(误差不超过
的一个正零点(误差不超过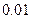 ).
).
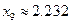 可作为所求函数的一个正零点的近似值
可作为所求函数的一个正零点的近似值
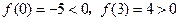 ,可取区间
,可取区间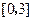 作为计算的初始区间.
作为计算的初始区间.| 端点(中点)坐标 |
计算中点的函数值 |
取区间 |
| |
|
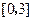 |
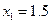 |
 |
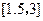 |
 |
 |
 |
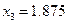 |
 |
 |
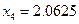 |
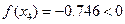 |
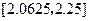 |
 |
 |
 |
 |
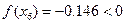 |
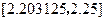 |
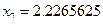 |
 |
 |
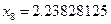 |
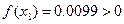 |
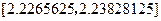 |
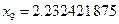 |
|
|