题目
(Ⅰ)当x∈[0,1]时,g(ax+2)>1恒成立,求a的取值范围;
(Ⅱ)设m(x)是定义在[s,t]上的函数,在(s,t)内任取n-1个数x1,x2,…,xn-2,xn-1,设x1<x2<…<xn-2<xn-1,令s=x0,t=xn,如果存在一个常数M>0,使得
| n |
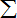 |
| i=1 |
试判断函数f(x)=|g(x)|在区间[
| 1 |
| a |
(注:
| n |
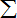 |
| i=1 |
答案
因为a>1,所以ax+2>a恒成立,即a-2<ax在区间[0,1]上恒成立,
所以a-2<1,即a<3,
所以1<a<3.即a的取值范围是(1,3).
(Ⅱ)由已知f(x)=|logax|,可知f(x)在[1,a2]上单调递增,在[
| 1 |
| a |
对于(
| 1 |
| a |
| 1 |
| a |
当存在某一个整数k∈{1,2,3,…,n-1},使得xk=1时,
| n |
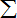 |
| i=1 |
| 1 |
| a |
当对于任意的k∈{0,1,2,3,…,n-1},xk≠1时,则存在一个实数k使得xk<1<xk+1,
此时
| n |
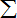 |
| i=1 |
=f(x0)-f(xk)+|f(xk)-f(xk+1)|+f(xn)-f(xk+1),(*)
当f(xk)>f(xk+1)时,(*)式=f(xn)+f(x0)-2f(xk+1)<3,
当f(xk)<f(xk+1)时,(*)式=f(xn)+f(x0)-2f(xk)<3,
当f(xk)=f(xk+1)时,(*)式=f(xn)+f(x0)-f(xk)-f(xk+1)<3.
综上,对于(
| 1 |
| a |
| 1 |
| a |
| n |
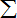 |
| i=1 |
所以存在常数M≥3,使
| n |
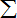 |
| i=1 |
所以函数f(x)在区间[
| 1 |
| a |
此时M的最小值为3.
