题目
| 2 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |
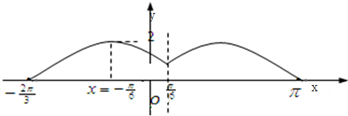
(Ⅰ)求函数y=f(x)在[-
| 2 |
| 3 |
(Ⅱ)求方程f(x)=
答案 | |||||||||||||||||||||||||||||||||||||||||
(Ⅰ)x∈[-
且f(x)=2sin(x+φ)过(-
∵0<φ<π,∴-
f(x)=2sin(x+
当
而函数y=f(x)的图象关于直线x=
∴f(x)=
|
| 2 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |

| 2 |
| 3 |
答案 | |||||||||||||||||||||||||||||||||||||||||
(Ⅰ)x∈[-
且f(x)=2sin(x+φ)过(-
∵0<φ<π,∴-
f(x)=2sin(x+
当
而函数y=f(x)的图象关于直线x=
∴f(x)=
|