题目

二次函数f(x)的二次项系数为正数，且对任意xÎR都有f(x)=f(4-x)成立，
若f(2－a²)<f(1+a－a²)，那么a的取值范围是                        (     )

A．1<a<2

B．a>1

C．a>2

D．a<1

答案

D

解析

试题分析：因为，二次函数f(x)的二次项系数为正数，且对任意xÎR都有f(x)=f(4-x)成立，所以二次函数图象开口向上，对称轴为x=2，而2－a²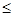2, 1+a－a²
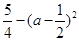
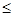
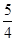=<2，故由f(2－a²)<f(1+a－a²)得，2－a²>1+a－a²,解得，a<1，选D。
点评：中档题，利用二次函数的图象和性质，将抽象不等式转化成具体不等式，利用不等式的解法等基础知识，达到解题目的。