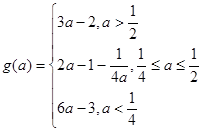题目
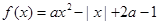 (
(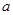 为实常数).
为实常数).(1)若
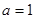 ,求函数
,求函数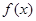 的单调区间;
的单调区间;(2)设
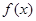 在区间
在区间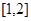 上的最小值为
上的最小值为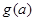 ,求
,求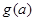 的表达式.
的表达式.
答案
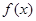 的单调递减区间为
的单调递减区间为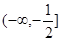 和
和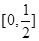 ;
;(2)
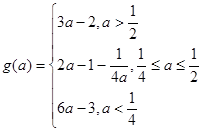 .
.
解析
试题分析:(1)根据绝对值的含义,取绝对值符号写出函数的分段形式;
(2)根据二次函数的对称轴方程与区间位置,分类讨论求最小值
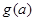 的解析式.
的解析式.(1)
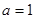 ,
,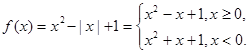
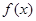 的单调递减区间为
的单调递减区间为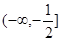 和
和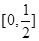 ;
;(2)当
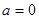 时,
时,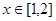 ,
,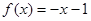 ,在
,在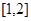 上单调递减,
上单调递减,所以当
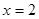 时,
时,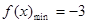 ;
;当
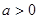 时,
时,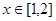 ,
,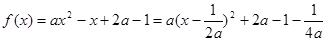 .
.(ⅰ)当
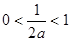 ,即
,即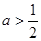 时,此时
时,此时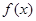 在
在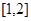 上单调递增,所以
上单调递增,所以 时,
时,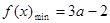 ;
;(ⅱ)当
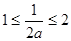 ,即
,即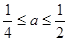 时,当
时,当 时,
时,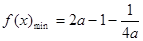 ;
;(ⅲ)当
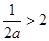 ,即
,即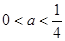 时,此时
时,此时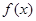 在
在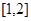 上单调递减,所以
上单调递减,所以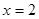 时,
时,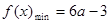
当
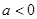 时,
时,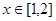 ,
,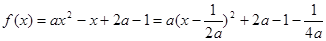 ,此时
,此时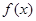 在
在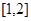 上单调递减,所以
上单调递减,所以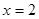 时,
时,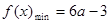 .
.综上: