题目
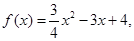 若
若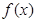 的定义域和值域都是
的定义域和值域都是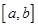 ,则
,则 .
.
答案
解析
试题分析:该二次函数开口向上,对称轴为
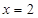 ,最小值为
,最小值为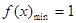 ,所以可分3种情况:
,所以可分3种情况:(1)当对称轴
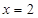 在区间
在区间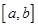 的左侧时,函数在区间
的左侧时,函数在区间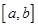 上单调递增,所以此时
上单调递增,所以此时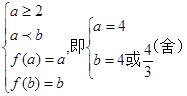 ;
;(2) 当对称轴
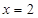 在区间
在区间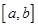 的右侧时,函数在区间
的右侧时,函数在区间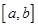 上单调递减,所以此时
上单调递减,所以此时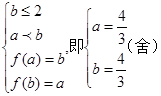 ;
;(3) 当对称轴
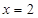 在区间
在区间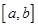 内时,函数在区间
内时,函数在区间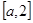 上单调递减,在区间
上单调递减,在区间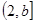 上单调递增,所以此时
上单调递增,所以此时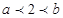 ,函数在区间
,函数在区间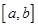 内的最小1值为1,也是值域的最小值
内的最小1值为1,也是值域的最小值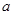 ,所以
,所以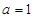 ,同时可知函数值域的最大值一定大于2.通过计算可知
,同时可知函数值域的最大值一定大于2.通过计算可知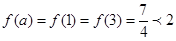 ,所以可知函数在
,所以可知函数在 时取得最大值
时取得最大值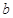 ,即
,即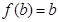 .所以
.所以 .
.通过验证可知,函数
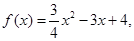 在区间
在区间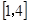 内的值域为
内的值域为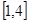 .
.综上可知:
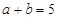 .
.
