题目
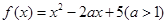 .
.(1)若
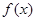 的定义域和值域均是
的定义域和值域均是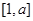 ,求实数
,求实数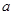 的值;
的值;(2)若
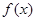 在区间
在区间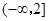 上是减函数,且对任意的
上是减函数,且对任意的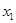 ,
,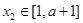 ,总有
,总有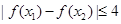 ,求实数
,求实数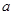 的取值范围.
的取值范围.
答案
 ;(2)
;(2)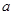 的取值范围是
的取值范围是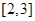 .
.
解析
试题分析:(1)根据条件
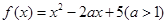 ,可知
,可知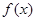 为二次函数,其对称轴为
为二次函数,其对称轴为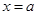 ,因此
,因此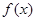 在
在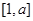 上是减函数,故根据条件
上是减函数,故根据条件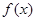 的定义域和值域均是
的定义域和值域均是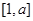 ,可列出关于
,可列出关于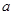 的方程组
的方程组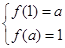 ,将
,将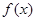 具体的表达式代入,即可求得
具体的表达式代入,即可求得 ;(2)首先根据条件可知
;(2)首先根据条件可知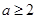 ,再由问题的描述,可将问题等价转化为求使对任意的
,再由问题的描述,可将问题等价转化为求使对任意的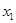 ,
,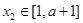 ,总有
,总有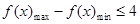 成立的
成立的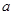 的取值范围,又由条件,二次函数
的取值范围,又由条件,二次函数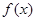 的对称轴
的对称轴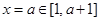 ,且左右端点
,且左右端点 对于对称轴
对于对称轴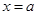 的偏离距离
的偏离距离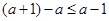 ,故有
,故有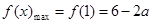 ,
,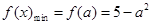 ,因此可以建立关于
,因此可以建立关于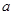 的不等式,从而求得
的不等式,从而求得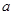 的取值范围是
的取值范围是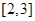 .
.试题解析:(1)∵
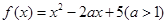 ,∴
,∴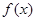 在
在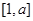 上是减函数 2分,
上是减函数 2分,又定义域和值域均为
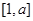 ,∴
,∴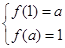 , 4分
, 4分即
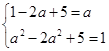 ,解得
,解得 . 5分;
. 5分; (2)∵
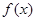 在区间
在区间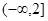 上是减函数,∴
上是减函数,∴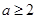 , 7分
, 7分又
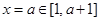 ,且
,且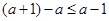 ,
,∴
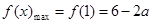 ,
,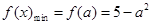 . 10分
. 10分∵对任意的
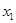 ,
,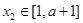 ,总有
,总有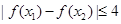 ,
,∴
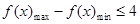 , 12分
, 12分即
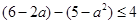 ,解得
,解得 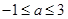 ,
,又∵
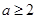 ,∴
,∴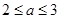 ,
,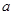 的取值范围是
的取值范围是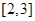 .
.
