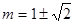题目
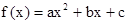 满足:
满足: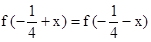 ,且
,且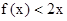 的
的解集为
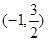
(1)求
 的解析式;
的解析式;(2)设
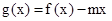
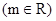 ,若
,若 在
在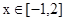 上的最小值为-4,求
上的最小值为-4,求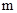 的值.
的值.
答案
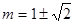
解析
试题分析:(1)由函数图象关于直线x=﹣
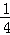 对称,得到a=2b,再由f(x)<2x的解集为
对称,得到a=2b,再由f(x)<2x的解集为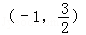 得到相应方程的根为x1=﹣1,x2=
得到相应方程的根为x1=﹣1,x2=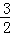 且a>0,结合根与系数的关系可得关于a、b、c方程组,由此联解即可得到a、b、c的值,从而得到求f(x)的解析式;
且a>0,结合根与系数的关系可得关于a、b、c方程组,由此联解即可得到a、b、c的值,从而得到求f(x)的解析式;(2)由(1)得函数g(x)=2x2+(1﹣m)x﹣3,图象关于直线x=
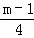 对称.因此分m<﹣3时、﹣3≤m≤9时和m>9时三种情况,根据函数的单调性列出各种情况下的最小值为4的式子,解出m的值并结合大前提进行取舍,最后综合即可得到符合题意的实数m的值.
对称.因此分m<﹣3时、﹣3≤m≤9时和m>9时三种情况,根据函数的单调性列出各种情况下的最小值为4的式子,解出m的值并结合大前提进行取舍,最后综合即可得到符合题意的实数m的值.试题分析:(1)∵
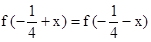 ∴
∴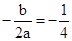 即
即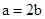 ①
① 又∵
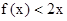 即
即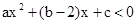 的解集为
的解集为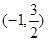
∴
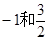 是
是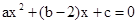 的两根且a>0.
的两根且a>0. ∴
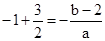 ②
②  ③
③由①②③得: a=2,b=1,c=-3
∴
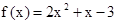
(2)
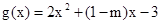 其对称轴方程为
其对称轴方程为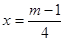
①若
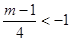 即m<-3时,
即m<-3时,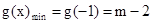
由
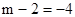 得
得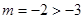 不符合题意
不符合题意 ②若
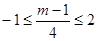 即
即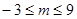 时,
时,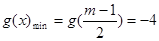 ,
,解得:
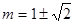 符合
符合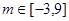
③若
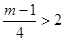 即m>9时,
即m>9时,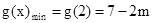
由
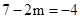 得
得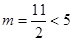 不符合题意
不符合题意∴