题目

已知二次函数f(x)=ax²+bx+c(a,b,c均为实数),满足a-b+c=0，对于任意实数x都有f (x)-x≥0，并且当x∈（0，2）时,有f (x)≤.
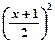（1）求f (1)的值；
（2）证明：ac≥；
（3）当x∈[-2，2]且a+c取得最小值时，函数F(x)=f (x)-mx (m为实数)是单调的，求证：m≤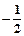或m≥.

答案

（1）f (1)=1.
（2）见解析
（3）见解析

解析

（1）∵对于任意x∈R，都有f (x)-x≥0,且当x∈(0,2)时,
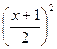有f (x) ≤.令x=1
∴1≤f (1) ≤.
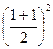即f (1)="1.·······················" 5分
（2） 由a-b+c=0及f (1)=1.
有,可得b=a+c=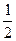.·············· 7分
又对任意x,f(x)-x≥0,即ax²-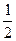x+c≥0.
∴a＞0且△≤0.
即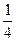-4ac≤0,解得ac≥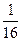.················ 9分
（3） 由(2)可知a＞0,c＞0.
a+c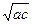≥2≥2·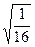=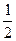.················ 10分
当且仅当时等号成立.此时
a=c=.························
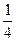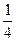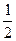∴f (x)= x²+x+,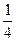
F (x)=f (x)-mx=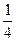[x²+(2-4m)x+1].············· 12分
当x∈[-2,2]时，f (x)是单调的，所以F (x)的顶点一定在[-2，2]的外边.
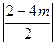∴≥2.····················· 13分
解得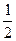m≤-或m≥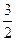. …………………………………………………………..14分