题目
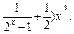
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)证明:f(x)>0.
答案
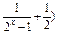 x3是偶函数(3)证明见解析
x3是偶函数(3)证明见解析
解析
 x≠0,∴定义域为(-∞,0)∪(0,+∞).
x≠0,∴定义域为(-∞,0)∪(0,+∞).(2)解 f(x)=(
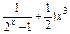
可化为f(x)=
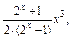
则f(-x)=
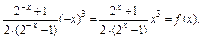
∴f(x)=(
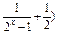 x3是偶函数.
x3是偶函数.(3)证明 当x>0时,2x>1,x3>0.
∴(
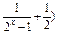 x3>0.
x3>0.∵f(x)为偶函数,∴当x<0时,f(x)=f(-x)>0.
综上可得f(x)>0.
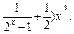
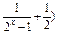 x3是偶函数(3)证明见解析
x3是偶函数(3)证明见解析
 x≠0,∴定义域为(-∞,0)∪(0,+∞).
x≠0,∴定义域为(-∞,0)∪(0,+∞).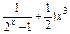
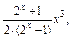
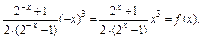
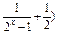 x3是偶函数.
x3是偶函数.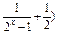 x3>0.
x3>0.