题目

.已知函数f(x)=x²+|x-a|+1,a∈R.
(1)试判断f(x)的奇偶性；
（2）若-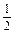≤a≤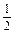，求f(x)的最小值.

答案

（1）f(x) 为非奇非偶函数（2）a²+1

解析

(1)当a=0时，函数f(-x)=(-x)²+|-x|+1=f(x),
此时,f(x)为偶函数.当a≠0时，f(a)=a²+1,f(-a)=a²+2|a|+1,
f(a)≠f(-a),f(a)≠-f(-a),此时，f(x) 为非奇非偶函数.
（2）当x≤a时,f(x)=x²-x+a+1=(x-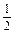)²+a+,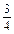
∵a≤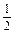,故函数f(x)在（-∞，a］上单调递减，
从而函数f(x)在（-∞，a］上的最小值为f(a)=a²+1.
当x≥a时，函数f(x)=x²+x-a+1=(x+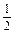)²-a+,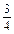
∵a≥-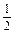，故函数f(x)在［a，+∞）上单调递增，从而函数f(x)在［a，+∞)上的最小值为f(a)=a²+1.
综上得，当-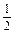≤a≤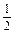时，函数f(x)的最小值为a²+1.