题目

已知函数f（x）=x²-2，g（x）=xlnx，，
（1）若对一切x∈（0，+∞），2g（x）≥ax-5-f（x）恒成立，求实数a的取值范围；
（2）试判断方程ln(1+x2)-

1

2

f(x)-k=0有几个实根．

答案

（1）若对一切x∈（0，+∞），2g（x）≥ax-5-f（x）恒成立，
即2xlnx+x²-ax+3≥0在x∈（0，+∞）恒成立，∴a≤2lnx+x+

3

x

在x∈（0，+∞）恒成立，
令F(x)=2lnx+x+

3

x

，则F′(x)=

2

x

+1-

3

x2

=

(x+3)(x-1)

x2

，F"（x）=0时x=1，F（x）在（0，1）递减，在（1，+∞）递增，∴F_min=F（1）=4，∴只需a≤4．
（2）将原方程化为ln(1+x2)-

1

2

x2+1=k，
令G(x)=ln(1+x2)-

1

2

x2+1，为偶函数，且G（0）=1，x＞0时G′(x)=

-x(x+1)(x-1)

x2+1

，

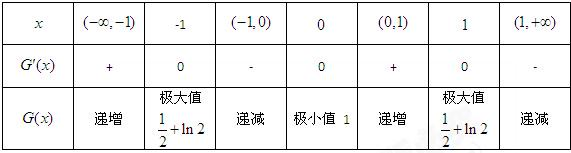
∴G（x）_max=

1

2

+ln2，且x→+∞，y→-∞∴k＞

1

2

+ln2时，无解；k=

1

2

+ln2或k=1时，三解；1＜k＜

1

2

+ln2，四解；k＜1时，两解．

解析