题目

已知奇函数f（x）的定义域是[-1，0）∪（0，1]，其在y轴右侧的图象如图所示，则不等式f（-x）-f（x）＜1的解集为（　　）

A．{x|- 1 2 ＜x＜0}	B．{x|- 1 2 ＜x＜0或0＜x≤1}
C．{x|-1≤x＜- 1 2 或0＜x≤1}	D．{x|-1≤x＜0或 1 2 ＜x≤1}

答案

∵奇函数f（x）的定义域是[-1，0）∪（0，1]，由图象知x∈（0，1]时，f（x）=-x+1
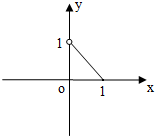
∴x∈[-1，0）时，f（x）=-x-1，
∵f（-x）-f（x）=-2f（x），f（-x）-f（x）＜1
即f（x）＞-

1

2

，
当x∈（0，1]时恒成立，
当x∈[-1，0）时，f（x）＞-

1

2

，即-x-1＞-

1

2

，
解得-1≤x＜-

1

2

，
综上所述，不等式f（-x）-f（x）＜1的解集为{x|-1≤x＜-

1

2

或0＜x≤1}，
故选C．

解析