题目

在给定的坐标系内作出函数f（x）=x²-1的图象，并回答下列问题
（Ⅰ）判断函数f（x）的奇偶性；
（Ⅱ）写出函数f（x）的单调减区间，并用函数单调性的定义证明．

答案

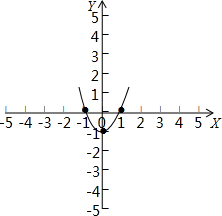
函数的图象如图：
（Ⅰ）∵f（x）=x²-1，
∴f（-x）=（-x）²-1=x²-1=f（x）．
∴f（x）是偶函数．
（Ⅱ）f（x）在[0，+∞）上递增，在（-∞，0）上递减．
任取x₁＜x₂≤0，
则f（x₁）-f（x₂）=x12-1-（x22-1）=（x₁-x₂）（x₁+x₂）．
∵x₁＜x₂≤0，
∴x₁-x₂＜0，x₁+x₂＜0．
∴f（x₁）-f（x₂）＞0．
∴f（x₁）＞f（x₂），
∴f（x）在（-∞，0）上递减．
因为函数为偶函数，
图象关于Y轴对称．
所以在[0，+∞）上递增．

解析