题目
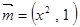 ,
,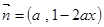 ,其中
,其中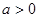 .函数
.函数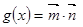 在区间
在区间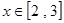 上有最大值为4,设
上有最大值为4,设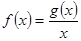 .
.(1)求实数
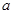 的值;
的值;(2)若不等式
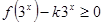 在
在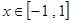 上恒成立,求实数
上恒成立,求实数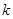 的取值范围.
的取值范围.
答案
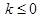 .
.
解析
试题分析:(1)
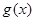 通过向量的数量积给出,利用数量积定义求出
通过向量的数量积给出,利用数量积定义求出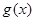 ,发现它是二次函数,利用二次函数的单调性可求出
,发现它是二次函数,利用二次函数的单调性可求出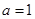 ;(2)由此
;(2)由此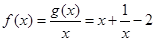 ,不等式
,不等式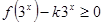 在
在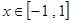 上恒成立,观察这个不等式,可以用换元法令
上恒成立,观察这个不等式,可以用换元法令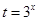 ,变形为
,变形为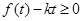 在
在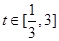 时恒成立,从而
时恒成立,从而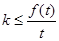 ,因此我们只要求出
,因此我们只要求出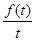 的最小值即可.下面我们要看
的最小值即可.下面我们要看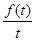 是什么函数,
是什么函数,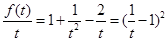 可以看作为关于
可以看作为关于 的二次函数,因此问题易解.
的二次函数,因此问题易解.试题解析:(1)由题得
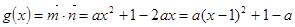
又
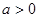 开口向上,对称轴为
开口向上,对称轴为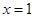 ,在区间
,在区间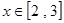 单调递增,最大值为4,
单调递增,最大值为4,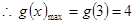
所以,
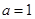
(2)由(1)的他,
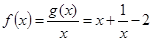
令
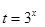 ,则
,则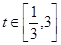 以
以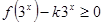 可化为
可化为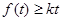 ,
,即
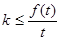 恒成立,
恒成立,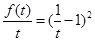 且
且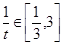 ,当
,当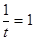 ,即
,即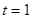 时
时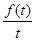 最小值为0,
最小值为0,