题目
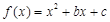 ,其中
,其中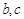 为常数.
为常数. (Ⅰ)若函数
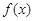 在区间
在区间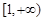 上单调,求
上单调,求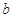 的取值范围;
的取值范围;(Ⅱ)若对任意
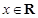 ,都有
,都有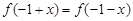 成立,且函数
成立,且函数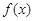 的图象经过点
的图象经过点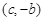 ,
,求
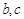 的值.
的值.
答案
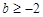 ;(Ⅱ)c=-1或c=-2.
;(Ⅱ)c=-1或c=-2.
解析
试题分析:(I)一元二次函数开口向上时,在对称轴的左侧单减,在对称轴的右侧单增,对称轴公式为x=
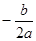 ,由题,
,由题,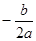 ≤1,解得
≤1,解得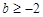 ;(Ⅱ)若
;(Ⅱ)若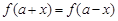 ,则f(x)关于x=a对称,由题,x=-1,所以b=2,将点(c,-b)代入解析式,有 c=-1或c=-2.
,则f(x)关于x=a对称,由题,x=-1,所以b=2,将点(c,-b)代入解析式,有 c=-1或c=-2.试题解析:(I)∵函数
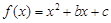 ,
,∴它的开口向上,对称轴方程为
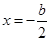 ,
,∵函数
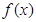 在区间
在区间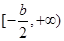 上单调递增,
上单调递增,∴
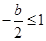 ,
,∴
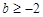 .
.(Ⅱ)∵
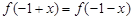 ,
,∴函数
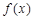 的对称轴方程为
的对称轴方程为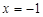 ,
,∴
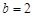 .
.又∵函数
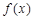 的图象经过点
的图象经过点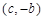 ,
,∴有
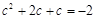 ,
,即
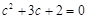 ,
,∴
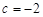 或
或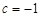 .
.
