题目
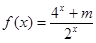 是奇函数.
是奇函数.(1)求m的值:
(2)设
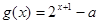 .若函数
.若函数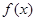 与
与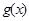 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围.
答案
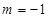 . (2)
. (2)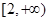 .
.
解析
试题分析:((1)由函数
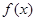 是奇函数可知:
是奇函数可知: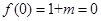 , 即得
, 即得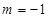 .
.(2)根据函数
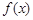 与
与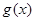 的图象至少有一个公共点,转化得到方程
的图象至少有一个公共点,转化得到方程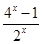
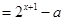 至少有一个实根.即方程
至少有一个实根.即方程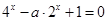 至少有一个实根 ,令
至少有一个实根 ,令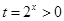 ,则方程
,则方程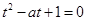 至少有一个正根.
至少有一个正根.接下来可有两种思路,一是通过分离参数,应用基本不等式;二是利用二次函数知识.
试题解析:(1)由函数
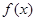 是奇函数可知:
是奇函数可知: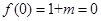 , 2分
, 2分解得
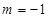 .4分
.4分(2)函数
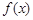 与
与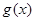 的图象至少有一个公共点
的图象至少有一个公共点即方程
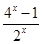
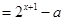 至少有一个实根6分
至少有一个实根6分即方程
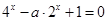 至少有一个实根8分
至少有一个实根8分令
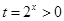 ,则方程
,则方程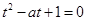 至少有一个正根
至少有一个正根 方法一:由于
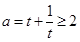
∴a的取值范围为
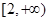 .12分
.12分方法二:令
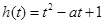 ,由于
,由于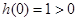 ,所以只须
,所以只须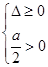 ,
,解得
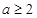 .
.∴a的取值范围为
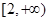 .
.
