题目
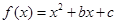 对任意实数均有
对任意实数均有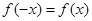 ,那么( )
,那么( )A.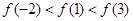
|
B.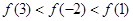
|
C.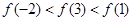
|
D.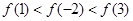
|
答案
解析
试题分析:因为函数
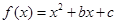 对任意实数均有
对任意实数均有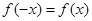 ,根据偶函数定义,可知函数
,根据偶函数定义,可知函数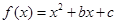 关于x=0对称,而利用二次函数的性质可知
关于x=0对称,而利用二次函数的性质可知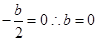 ,故可知
,故可知 ,开口向上,距离对称轴越远的函数值越大,则可知3>|-2|>1,因此可知
,开口向上,距离对称轴越远的函数值越大,则可知3>|-2|>1,因此可知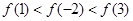 ,故选D.
,故选D.点评:解决该试题的关键是理解二次函数是一个偶函数,充分说明其对称轴为x=0,得到b的值。然后结合单调性来分析大小关系。
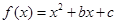 对任意实数均有
对任意实数均有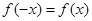 ,那么( )
,那么( )A.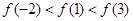
|
B.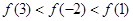
|
C.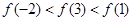
|
D.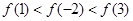
|
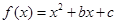 对任意实数均有
对任意实数均有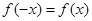 ,根据偶函数定义,可知函数
,根据偶函数定义,可知函数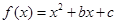 关于x=0对称,而利用二次函数的性质可知
关于x=0对称,而利用二次函数的性质可知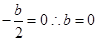 ,故可知
,故可知 ,开口向上,距离对称轴越远的函数值越大,则可知3>|-2|>1,因此可知
,开口向上,距离对称轴越远的函数值越大,则可知3>|-2|>1,因此可知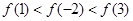 ,故选D.
,故选D.