题目

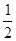（12分）二次函数f(x)与g(x)=x²－1的图像开口大小相同，开口方向也相同，y=f(x)的对称轴方程为x=1，图像过点(2, 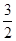)点
（1）求f(x)的解析式；
（2）是否存在大于1的实数m，使y=f(x)在[1, m]上的值域是［1, m］？若存在，求出m的值，若不存在，说明理由.

答案

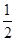（1）f(x)= (x－1)²+1；（2）存在m=3符合题意.

解析

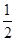第一问根据开口大小相同，开口方向相同可以确定两二次函数的二次项系数相同，所以可设f(x)=(x－1)²+k，将点代入就可求出。第二问根据函数的单调性可以确定f(m)=m，解出来与1比较大小就可以确定m是否存在。
解：（1）由题意设f(x)=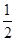(x－1)²+k 代入(2, 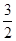)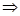k=1
∴f(x)= 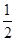(x－1)²+1
（2）假设存在，则y=f(x)在[1, m]上↑
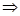f(m)=m
即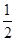(m－1)²+1=m
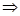m="1," m=3
又m>1
∴ m=3
存在m=3符合题意.