题目

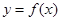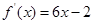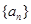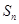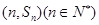已知二次函数的图像经过坐标原点，其导函数为，数列的前n项和为，点均在函数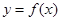的图像上。
（Ⅰ）、求数列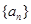的通项公式；        
（Ⅱ）、设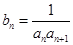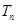，是数列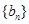的前n项和，求使得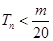对所有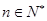都成立的最小正整数m；

答案

（Ⅰ）a_n＝6n－5 （）
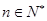（Ⅱ）满足要求的最小正整数m为10.

解析

本小题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能，考查分析问题的能力和推理能力。
（1）设这二次函数f（x）=ax2+bx（a≠0），根据导函数求得f（x）的表达式，再根据点（n，Sn）（n∈N*）均在函数
y=f（x）的图象上，求出an的递推关系式，
（2）把（1）题中an的递推关系式代入bn，根据裂项相消法求得Tn，最后解得使得Tn＜ 
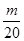
对所有n∈N*都成立的最小正整数m