题目
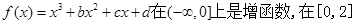 上是减函数,且
上是减函数,且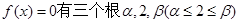 。
。(1)求
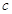 的值,并求出
的值,并求出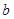 和
和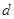 的取值范围。
的取值范围。(2)求证
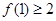 。
。(3)求
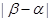 的取值范围,并写出当
的取值范围,并写出当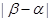 取最小值时的
取最小值时的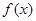 的解析式。
的解析式。
答案
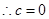 b≤-3
b≤-3 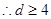 (2)略
(2)略(3)
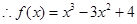
解析
(1)因为
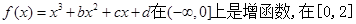 上是减函数,且
上是减函数,且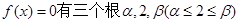 ,结合韦达定理和单调性得到范围。
,结合韦达定理和单调性得到范围。(2)
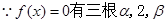 故有
故有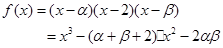 ,让,后利用根与系数的关系得到解析式
,让,后利用根与系数的关系得到解析式
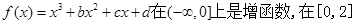 上是减函数,且
上是减函数,且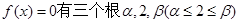 。
。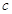 的值,并求出
的值,并求出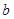 和
和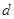 的取值范围。
的取值范围。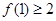 。
。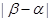 的取值范围,并写出当
的取值范围,并写出当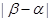 取最小值时的
取最小值时的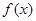 的解析式。
的解析式。
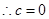 b≤-3
b≤-3 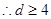 (2)略
(2)略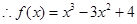
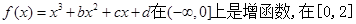 上是减函数,且
上是减函数,且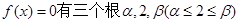 ,结合韦达定理和单调性得到范围。
,结合韦达定理和单调性得到范围。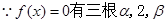 故有
故有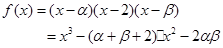 ,让,后利用根与系数的关系得到解析式
,让,后利用根与系数的关系得到解析式