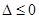题目
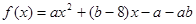 ,当
,当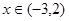 时,
时,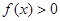 ;
;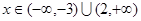 时,
时,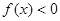
(1)求
 的解析式.
的解析式.(2)c为何值时,
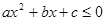 的解集为R.
的解集为R.
答案
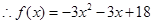
⑵当
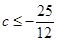 时
时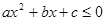 的解集为R.
的解集为R.
解析
(1)由
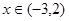 时,
时,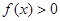 ;
;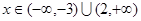 时,
时,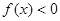
知:
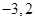 是是方程
是是方程 的两根,那么利用根与系数的关系得到a,b的值。
的两根,那么利用根与系数的关系得到a,b的值。(2)由于由
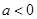 ,知二次函数
,知二次函数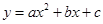 的图象开口向下
的图象开口向下要使
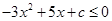 的解集为R,只需
的解集为R,只需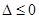
那么可知参数的范围。
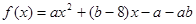 ,当
,当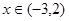 时,
时,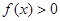 ;
;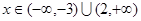 时,
时,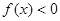
 的解析式.
的解析式.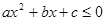 的解集为R.
的解集为R.
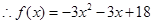
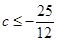 时
时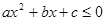 的解集为R.
的解集为R.
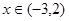 时,
时,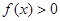 ;
;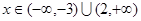 时,
时,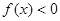
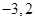 是是方程
是是方程 的两根,那么利用根与系数的关系得到a,b的值。
的两根,那么利用根与系数的关系得到a,b的值。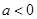 ,知二次函数
,知二次函数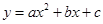 的图象开口向下
的图象开口向下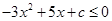 的解集为R,只需
的解集为R,只需