题目
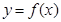 是二次函数,方程
是二次函数,方程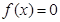 有两相等实根,且
有两相等实根,且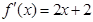
(1)求
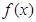 的解析式.
的解析式.(2)求函数
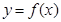 与函数
与函数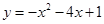 所围成的图形的面积.
所围成的图形的面积.
答案
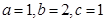 ,
,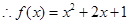 ;
;(2)
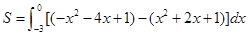
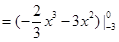 =9 .
=9 .
解析
(1)设
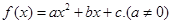 有判别式和导数的斜率得到参数a,b的值,进而求解解析式。
有判别式和导数的斜率得到参数a,b的值,进而求解解析式。(2)由题
 或
或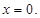 ,再用定积分表示面积
,再用定积分表示面积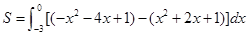 求解得到。
求解得到。解:(1)设
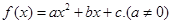 .由题意得
.由题意得 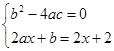
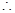
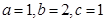
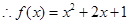 -………6分
-………6分(2)由题
 或
或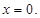 ………8分
………8分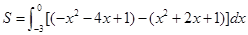
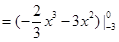 =9 . ………12分
=9 . ………12分
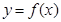 是二次函数,方程
是二次函数,方程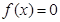 有两相等实根,且
有两相等实根,且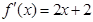
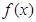 的解析式.
的解析式.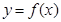 与函数
与函数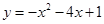 所围成的图形的面积.
所围成的图形的面积.
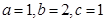 ,
,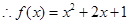 ;
;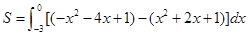
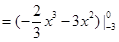 =9 .
=9 .
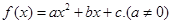 有判别式和导数的斜率得到参数a,b的值,进而求解解析式。
有判别式和导数的斜率得到参数a,b的值,进而求解解析式。 或
或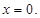 ,再用定积分表示面积
,再用定积分表示面积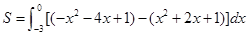 求解得到。
求解得到。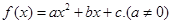 .由题意得
.由题意得 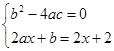
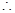
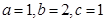
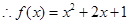 -………6分
-………6分 或
或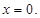 ………8分
………8分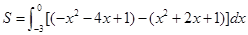
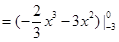 =9 . ………12分
=9 . ………12分