题目

如图，已知二次函数y=（x+m）²+k-m²的图象与x轴相交于两个不同的点A（x₁，0）、B（x₂，0），与y轴的交点为C．设△ABC的外接圆的圆心为点P．
（1）求⊙P与y轴的另一个交点D的坐标；
（2）如果AB恰好为⊙P的直径，且△ABC的面积等于，求m和k的值．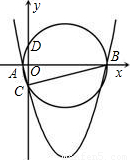

答案

（1）（0，1） （2）k=-1，m=-2

解析

解：（1）易求得点C的坐标为（0，k）
由题设可知x₁，x₂是方程（x+m）²+k-m²=0即x²+2mx+k=0的两根，
所以x_1，2=，
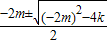所x₁+x₂=-2m，x₁•x₂=k（1分）
如图，∵⊙P与y轴的另一个交点为D，由于AB、CD是⊙P的两条相交弦，设它们的交点为点O，连接DB，

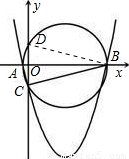
∴△AOC∽△DOB，则OD=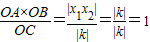（2分）
由题意知点C在y轴的负半轴上，从而点D在y轴的正半轴上，
所以点D的坐标为（0，1）（3分）
（2）∵AB⊥CD，AB又恰好为⊙P的直径，则C、D关于点O对称，
所以点C的坐标为（0，-1），
即k=-1（4分）
又AB=|x₂-x₁|==，
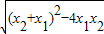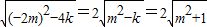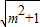所以S_△ABC=AB×OC=×2×1=，
解得m=±2．（正值舍去）
∴k=-1，m=-2．