题目
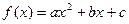
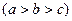 ,点
,点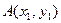 、
、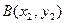 是该函数图象上的两点,且满足
是该函数图象上的两点,且满足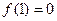 ,
,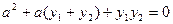 ;
;(1)、求证:
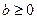 ;
;(2)、问是否能够保证
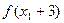 和
和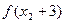 中至少有一个为正数?请证明你的结论。
中至少有一个为正数?请证明你的结论。
答案
解析
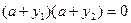 ,则
,则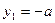 或
或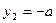 ,
,则方程
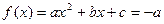 有实根,即方程
有实根,即方程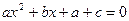 有实根,
有实根,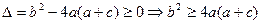 ,
,又
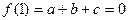 且
且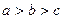 ,则
,则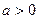 、
、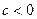 、
、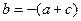 ,
,则
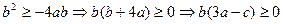 ,
,由于
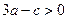 ,则
,则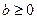 ;
;(2)、依题意,
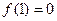 ,即1是方程
,即1是方程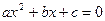 的一个根,则另一个根为
的一个根,则另一个根为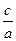 ,且
,且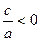 ,则有
,则有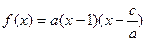 ,不妨设
,不妨设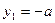 ,
,即:
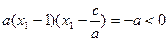 ,∴
,∴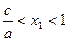 ,∴
,∴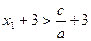 (◆)
(◆)又由
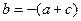 及
及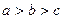 得
得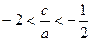 ,
,∴
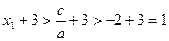 ,
,而函数
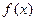 在
在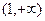 上为增函数,∴
上为增函数,∴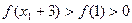 ,
,同理,若
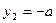 ,则有
,则有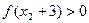 ,命题得证。
,命题得证。
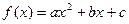
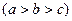 ,点
,点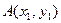 、
、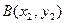 是该函数图象上的两点,且满足
是该函数图象上的两点,且满足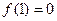 ,
,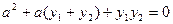 ;
;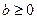 ;
;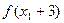 和
和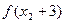 中至少有一个为正数?请证明你的结论。
中至少有一个为正数?请证明你的结论。
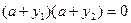 ,则
,则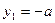 或
或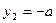 ,
,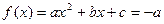 有实根,即方程
有实根,即方程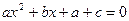 有实根,
有实根,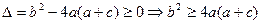 ,
,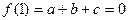 且
且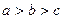 ,则
,则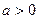 、
、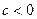 、
、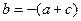 ,
,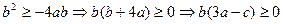 ,
,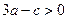 ,则
,则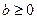 ;
;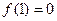 ,即1是方程
,即1是方程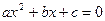 的一个根,则另一个根为
的一个根,则另一个根为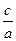 ,且
,且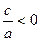 ,则有
,则有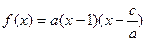 ,不妨设
,不妨设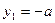 ,
,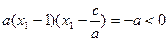 ,∴
,∴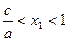 ,∴
,∴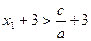 (◆)
(◆)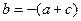 及
及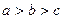 得
得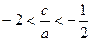 ,
,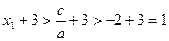 ,
,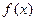 在
在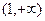 上为增函数,∴
上为增函数,∴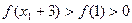 ,
,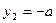 ,则有
,则有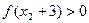 ,命题得证。
,命题得证。