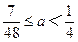题目
(1)证明:(1+x1)(1+x2)=1;
(2)证明:x1<-1,x2<-1;
(3)若函数y=xf(x)在区间(-
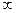 ,-4)
,-4) 上单调递增,试求a的取值范围。
上单调递增,试求a的取值范围。
答案
解析
 1)由题意知x1,x2是一元二次方和ax2+x+1=0的两个实根,所以x1+x2=-
1)由题意知x1,x2是一元二次方和ax2+x+1=0的两个实根,所以x1+x2=-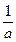 ,x1x2=
,x1x2=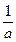
x1+x2=-x1x2,所以(1+x1)(1+x2)=1
(2)由方程ax2+x+1=0(a>0)的判别式
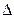 =1-4a>0,解得0<a<
=1-4a>0,解得0<a<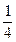 .
.所以y=ax2+x+1=0(a>0)的图象的对
 称轴
称轴x=-
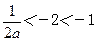 ,且f(-1)=a>0
,且f(-1)=a>0所以二次函数y=ax2+x+1(a>0)的图象与x轴两个交点都在-1点的左侧,
即x1<-1,x2<-1
(3)设g(x)=xf(x)=ax3+x2+x(0<a<
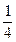 ),
),∴g’(x)=3ax2+2x+1>0对x
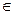 (-
(-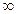 ,-4)恒成立,
,-4)恒成立,∴3a>
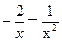 =-(
=-(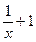 )2+1
)2+1又当x
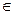 (-
(-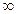 ,-4)时,-(
,-4)时,-(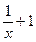 )2+1<
)2+1<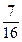
∴a≥
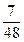 ,∴
,∴