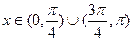题目
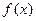 对任意的
对任意的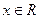 都有
都有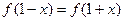 ,设向量
,设向量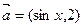 ,
,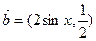 ,
,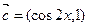 ,
,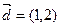 ,当
,当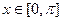 时,求
时,求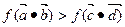 解集
解集
答案
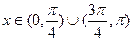
解析
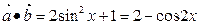 ,
,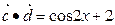
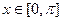 时,
时,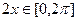 ,所以
,所以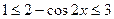 ,
,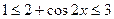
所以
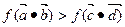
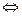
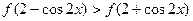
由
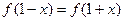 可知函数
可知函数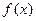 的对称轴为
的对称轴为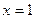
(1)若开口向上,则
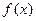 在
在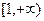 单调递增,则不等式可化为
单调递增,则不等式可化为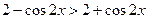
即
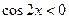 ,所以
,所以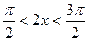 ,
,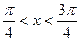 ,原不等式解集为
,原不等式解集为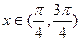
(2)若开口向下,则
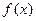 在
在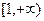 单调递减,则不等式可化为
单调递减,则不等式可化为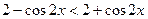
即
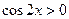 ,所以
,所以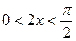 或
或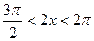 ,原不等式解集为
,原不等式解集为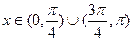
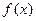 对任意的
对任意的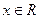 都有
都有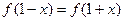 ,设向量
,设向量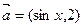 ,
,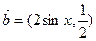 ,
,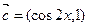 ,
,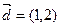 ,当
,当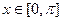 时,求
时,求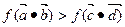 解集
解集
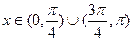
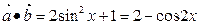 ,
,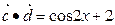
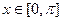 时,
时,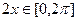 ,所以
,所以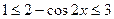 ,
,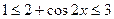
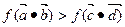
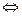
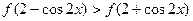
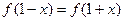 可知函数
可知函数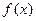 的对称轴为
的对称轴为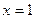
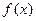 在
在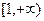 单调递增,则不等式可化为
单调递增,则不等式可化为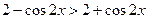
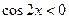 ,所以
,所以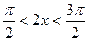 ,
,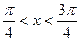 ,原不等式解集为
,原不等式解集为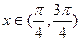
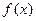 在
在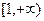 单调递减,则不等式可化为
单调递减,则不等式可化为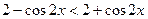
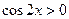 ,所以
,所以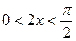 或
或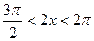 ,原不等式解集为
,原不等式解集为