题目

设二次函数f(x)=ax²+bx+c(a＞0)，方程f(x)－x=0的两个根x₁、x₂满足0＜x₁＜x₂＜。
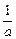(1)当x∈［0，x₁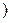时，证明x＜f(x)＜x₁；
(2)设函数f(x)的图像关于直线x=x₀对称，证明：x₀＜。

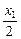答案

(1)证明略， (2)证明略

解析

(1)令F(x)=f(x)－x，因为x₁，x₂是方程f(x)－x=0的根，所以F(x)=a(x－x₁)(x－x₂). 当x∈(0，x₁)时，由于x₁＜x₂，得(x－x₁)(x－x₂)＞0，
又a＞0，得F(x)=a(x－x₁)(x－x₂)＞0，即x＜f(x)
x₁－f(x)=x₁－［x+F(x)］=x₁－x+a(x₁－x)(x－x₂)=(x₁－x)［1+a(x－x₂)］
∵0＜x＜x₁＜x₂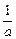＜，∴x₁－x＞0，1+a(x－x₂)=1+ax－ax₂＞1－ax₂＞0
∴x₁－f(x)＞0，由此得f(x)＜x₁.
(2)依题意: x₀=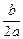－，因为x₁、x₂是方程f(x)－x=0的两根，即x₁，x₂是方程ax²+(b－1)x+c=0的根.
∴x₁+x₂=－
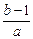
∴x₀=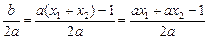－，因为ax₂＜1，
∴x₀＜.
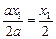