题目

答案
解析
判定的条件是p:
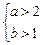 ,结论是q:
,结论是q: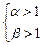
(注意p中a、b满足的前提是Δ=a2-4b≥0)
(1)由
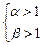 ,得a=α+β>2,b=αβ>1,∴q
,得a=α+β>2,b=αβ>1,∴q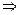 p
p(2)为证明p
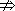 q,可以举出反例
q,可以举出反例 取α=4,β=
取α=4,β=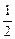 ,它满足a=α+β=4+
,它满足a=α+β=4+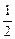 >2,b=αβ=4×
>2,b=αβ=4×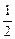 =2>1,但q不成立.
=2>1,但q不成立.综上讨论可知a>2,b>1是α>1,β>1的必要但不充分条件.

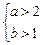 ,结论是q:
,结论是q: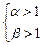
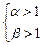 ,得a=α+β>2,b=αβ>1,∴q
,得a=α+β>2,b=αβ>1,∴q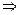 p
p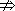 q,可以举出反例
q,可以举出反例 取α=4,β=
取α=4,β=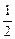 ,它满足a=α+β=4+
,它满足a=α+β=4+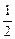 >2,b=αβ=4×
>2,b=αβ=4×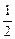 =2>1,但q不成立.
=2>1,但q不成立.