题目

已知函数f(x)的定义域为R，且满足f(x+2)=-f(x).
（1）求证：f(x)是周期函数；
（2）若f(x)为奇函数，且当0≤x≤1时，f(x)=x,求使f(x)=-在［0，2 009］上的所有x的个数.

答案

（1）证明见解析（2）在［0，2 009］上共有502个x使f(x)="-"

解析

（1）证明 ∵f（x+2）=-f（x），
∴f（x+4）=-f（x+2）=-［-f（x）］=f（x）， 2分
∴f（x）是以4为周期的周期函数， 4分
（2）解 当0≤x≤1时，f(x)=x,
设-1≤x≤0,则0≤-x≤1,∴f（-x）=（-x）=-x.
∵f(x)是奇函数，∴f（-x）=-f（x）,
∴-f（x）=-x，即f(x)=x.  7分
故f(x)= x(-1≤x≤1) 8分
又设1＜x＜3,则-1＜x-2＜1,
∴f(x-2)= (x-2),10分
又∵f（x-2）=-f（2-x）=-f（（-x）+2）=-［-f（-x）］=-f（x），
∴-f（x）=（x-2），
∴f（x）=-（x-2）（1＜x＜3）.  11分
∴f（x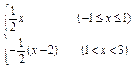）= 12分
由f(x)="-" ,解得x=-1.
∵f（x）是以4为周期的周期函数.
∴f(x)="-" 的所有x="4n-1" (n∈Z). 14分
令0≤4n-1≤2 009,则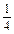≤n≤,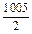
又∵n∈Z，∴1≤n≤502 （n∈Z）,
∴在［0，2 009］上共有502个x使f(x)="-" . 16分