题目

判断下列函数的奇偶性.
（1）f(x)=;
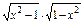(2)f(x)=log₂(x+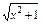) (x∈R);
(3)f(x)=lg|x-2|.

答案

（1）f(x)既是奇函数又是偶函数（2）f(x)是奇函数（3）f(x)为非奇非偶函数

解析

（1）∵x²-1≥0且1-x²≥0,∴x=±1,即f(x)的定义域是{-1，1}.
∵f（1）=0，f(-1)=0,∴f(1)=f(-1),f(-1)=-f(1),故f(x)既是奇函数又是偶函数.
（2）方法一 易知f(x)的定义域为R，
又∵f(-x)=log₂［-x+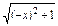］=log₂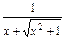=-log₂(x+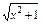)=-f(x),
∴f(x)是奇函数.
方法二 易知f(x)的定义域为R，
又∵f（-x）+f（x）=log₂［-x+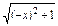］+log₂(x+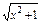)=log₂1=0,即f(-x)=-f(x),
∴f(x)为奇函数.
（3）由|x-2|＞0，得x≠2.
∴f（x）的定义域{x|x≠2}关于原点不对称，故f(x)为非奇非偶函数.