题目
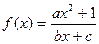 (a、b、c∈Z)是奇函数,又
(a、b、c∈Z)是奇函数,又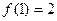 ,
,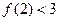 ,求a、b、c的值.
,求a、b、c的值.
答案
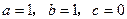
解析
∴c=0,由f(1)=2,得a+1=2b,由f(2)<3,得
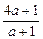 <3,
<3,解得-1<a<2.又a∈Z,∴a=0或a=1.若a=0,则b=
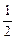 ,与b∈Z矛盾.∴a=1,b=1,c=0.
,与b∈Z矛盾.∴a=1,b=1,c=0.
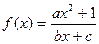 (a、b、c∈Z)是奇函数,又
(a、b、c∈Z)是奇函数,又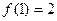 ,
,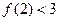 ,求a、b、c的值.
,求a、b、c的值.
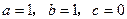
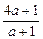 <3,
<3,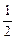 ,与b∈Z矛盾.∴a=1,b=1,c=0.
,与b∈Z矛盾.∴a=1,b=1,c=0.