题目
(i)f(x1-x2)=
 ;
;(ii)存在正常数a使f(a)=1
 求证:
求证: (1)f(x)是奇函数.
(2)f(x)是周期函数,且有一个周期是4.
答案
解析
则f(-x)=f(x2-x1)=

=-f(x1-x2)=-f(x)

∴f(x)是奇函数.
(2)要证f(x+4a)=f(x),可先计算f(x+a),f(x+2a).
∵f(x+a)=f[x-(-a)]=


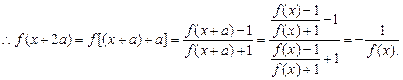
∴f(x+4a)=f[(x+2a)+2a]=
 =f(x),
=f(x),故f(x)是以4a为周期的周期函数.
 ;
; 求证:
求证: 



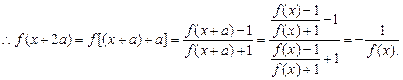
 =f(x),
=f(x),