题目

已知函数f（x）=ax³+bx²+cx+d满足f（0）=f（x₁）=f（x₂）=0，且0＜x₁＜x₂．若f（x）在（x₂，+∞）上是增函数，则b的取值范围是______．

答案

∵f（0）=0∴d=0，∴f（x）=ax³+bx²+cx=x（ax²+bx+c），又f（x₁）=f（x₂）=0，且0＜x₁＜x₂，∴x₁，x₂是ax²+bx+c=0两根，且a≠0．
由韦达定理x₁+x₂ =-

b

a

＞0，①
∴f（x）=ax³+bx²+cx+d的大致图象为：
当a＞0时


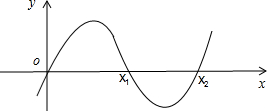
由图，f（x）在（x₂，+∞）上是增函数，由①得，b＜0
②当a＜0时，


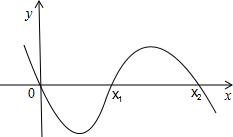
f（x）在（x₂，+∞）上不是增函数，不合题意．
故答案为：b＜0

解析