题目
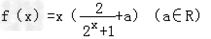 .
.(1)求实数a使函数f(x)为偶函数?
(2)对于(1)中的a的值,求证:f(x)≤0恒成立.
答案
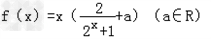 为偶函数
为偶函数∴f(﹣x)=f(x)对于任意的x都成立
∴﹣x(
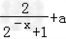 )=x(
)=x(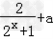 )
)整理可得,(2+2a)●x=0对于任意x都成立
∴a=﹣1
(2)证明:当a=﹣1时,f(x)=x(
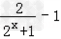 )
)(i)当x=0时,f(x)=0
(ii)当x>0时,2x+1>2
∴
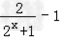 <0
<0∴f(x)<0
(iii)当x<0时,0<2x+1<2
∴
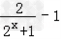 >0
>0∴f(x)<0
综上可得,f(x)≤0
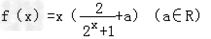 .
.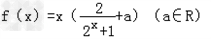 为偶函数
为偶函数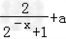 )=x(
)=x(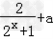 )
)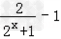 )
)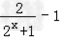 <0
<0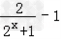 >0
>0