题目

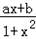设函数f（x）=是定义在（﹣1，1）上的奇函数，且 f（）=
（1）确定函数f（x）的解析式
（2）用定义证明f（x）在（﹣1，1）上是增函数
（3）解不等式f （t﹣1）+f（t）＜0．

答案

解：（1）由已知得f（﹣x）=﹣f（x），
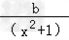∴﹣ax+=﹣ax﹣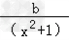，解得b=0，
则f（x）=ax﹣；
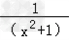又f（）=，
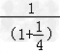∴=﹣，解得a=1．
∴f（x）=．
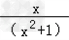（2）设﹣1＜x₁＜x₂＜1，
则f（x₂）﹣f（x₁）=﹣=，
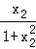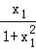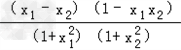显然f（x₂）﹣f（x₁）＞0，
∴f（x）在（﹣1，1）上单调递增．
（3）原式化为f（t﹣1）＜﹣f（t），又f（x）是奇函数，
∴f（t﹣1）＜f（﹣t），由已知得：
﹣1＜t﹣1＜1，
﹣1＜﹣t＜1，
t﹣1＜﹣t，
解得t∈（0，）．

解析