题目

已知f（x）是以2为周期的偶函数，当x∈[0，1]时，f（x）=x，那么在区间[-1，3]内，关于x的方程f（x）=kx+k+1（k∈R且k≠-1）有4个不同的根，则k的取值范围是（　　）

A．(- 1 4 ，0)

B．（-1，0）

C．(- 1 2 ，0)

D．(- 1 3 ，0)

答案

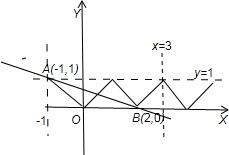
因为关于x的方程f（x）=kx+k+1（k∈R且k≠-1）有4个不同的根，
就是函数f（x）的图象与y=kx+k+1的图象有4个不同的交点，
f（x）是以2为周期的偶函数，当x∈[0，1]时，f（x）=x，
所以可以得到函数f（x）的图象
又因为y=kx+k+1=k（x+1）+1过定点（-1，1），
在同一坐标系内画出它们的图象如图，
由图得y=kx+k+1=k（x+1）+1在直线AB和y=1中间时符合要求，
而k_AB=-

1

3

所以k的取值范围是-

1

3

＜k＜0
故选D．

解析